Sketch the Graph of a Function F That is Continuous on 1 5
HOW TO SKETCH THE GRAPH AND FIND CONTINUITY OF FUNCTIONS
About "How to Sketch the Graph and Find Continuity of Functions"
How to Sketch the Graph and Find Continuity of Functions :
Here we are going to see some example problems to understand the concept of sketching the graph and verifying the continuity of the function.
Sketch the Graph and Verify the Continuity of the Function - Practice questions
Question 1 :
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
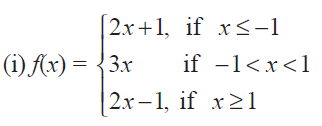
Solution :
First let us check the continuity at the point x = -1
lim x-> -1- f(x) = limx-> -1- 2x + 1
By applying the limit, we get
= 2(-1) + 1
= -2 + 1
= -1 -----(1)
limx-> -1+ f(x) = limx-> -1+ 3x
By applying the limit, we get
= 3(-1)
= -3 -----(2)
lim x-> -1- f(x) ≠ limx-> -1+
So, the function is not continuous at x = -1.
Now let us check the continuity at the point x = 1
limx-> 1- f(x) = limx-> 1- 3x
By applying the limit, we get
= 3(1)
= 3 -----(1)
limx-> -1+ f(x) = limx-> -1+ 2x - 1
By applying the limit, we get
= 2(1) - 1
= 1 -----(2)
lim x-> 1- f(x) ≠ limx-> 1+
So, the function is not continuous at x = 1.
To find at which of these points f is continuous from the right, from the left, or neither, we have to draw the number line.
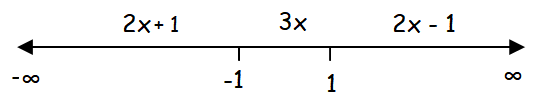
let x0∈ (- ∞, -1]
lim x-> x0 f(x) = limx-> x0 2x + 1
Applying the limit, we get
= 2x0 + 1 ------(1)
f(x0) = 2x0 + 1 ------(2)
(1) = (2)
It is continuous in (- ∞, -1].
letx0∈ (-1 , -1)
limx-> x0 f(x) = limx-> x0 3x
Applying the limit, we get
= 3x0 ------(1)
f(x0) = 3x0 ------(2)
(1) = (2)
It is continuous in (-1 , 1).
letx0∈ [1 , ∞ )
limx-> x0 f(x) = limx-> x0 2x - 1
Applying the limit, we get
= 2x0 - 1 ------(1)
f(x0) =2x 0 - 1 ------(2)
(1) = (2)
It is continuous in [1 , ∞ ).
Graph of f(x) = 2x + 1 :
| x = -1 f(-1) = -1 | x = -2 f(-2) = -3 | x = -3 f(-3) = -5 |
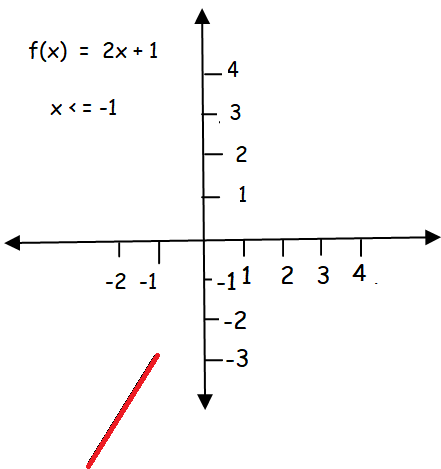
Graph of f(x) = 3x :
-1 < x < 1
| x = -0.5 f(-0.5) = -1.5 | x = -0.7 f(-0.7) = -2.1 | x = 0.5 f(0.5) = 1.5 |
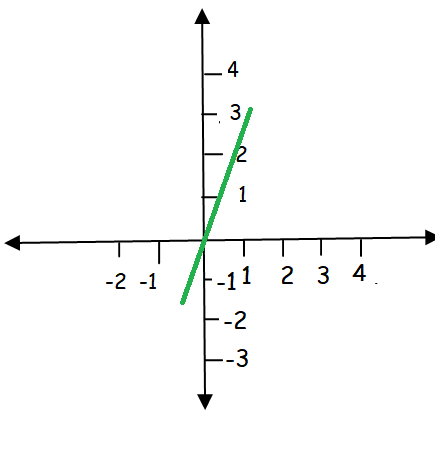
Graph of f(x) = 2x - 1:
x > = 1
| x = 1 f(1) = 1 | x = 2 f(2) = 3 | x = 3 f(3) = 5 |
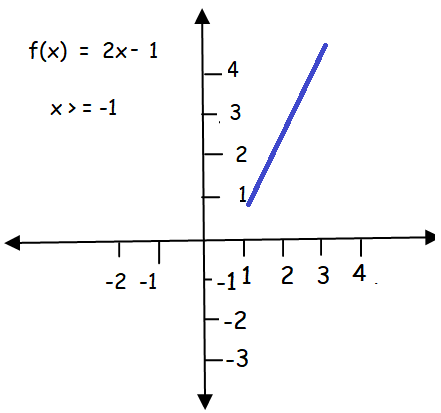
Question 2 :
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
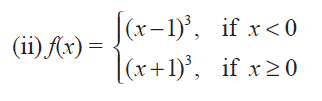
Solution :
First let us check the continuity at the point x = 0
limx-> 0- f(x) = limx-> 0- (x - 1)3
By applying the limit, we get
= (0 - 1)3
= -1 -----(1)
limx-> 0+ f(x) = limx-> 0+ (x + 1)3
By applying the limit, we get
= ( 0 + 1)3
= 1 -----(2)
lim x-> 0- f(x) ≠ limx-> 0+
So, the function is not continuous at x = 0.
To find at which of these points f is continuous from the right, from the left, or neither, we have to draw the number line.
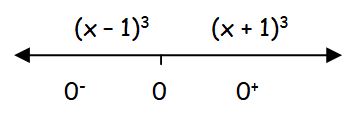
letx0∈ (- ∞, 0]
limx-> x0 f(x) = limx-> x0 (x - 1)3
Applying the limit, we get
= (x0 - 1)3 ------(1)
f(x0) = (x0 - 1)3 ------(2)
(1) = (2)
It is continuous in (- ∞, 0].
letx0∈ [0 , ∞ )
limx-> x0 f(x) = limx-> x0 (x + 1)3
Applying the limit, we get
= (x0 + 1)3 ------(1)
f(x0) = (x0 + 1)3 ------(2)
(1) = (2)
It is continuous in [0, ∞ ) .
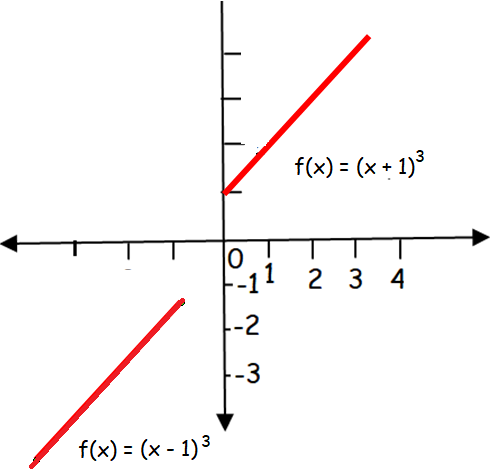
Graph of f(x) = (x - 1)3
x < 0
| x = -1 f(-1) = -8 | x = -2 f(-2) = -27 | x = -3 f(-3) = -64 |
Graph of f(x) = (x + 1)3
x >= 0
| x = 1 f(1) = 8 | x = 2 f(2) = 27 | x = 3 f(3) = 64 |

After having gone through the stuff given above, we hope that the students would have understood, " How to Sketch the Graph and Find Continuity of Functions"
Apart from the stuff given in " How to Sketch the Graph and Find Continuity of Functions" , if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback tov4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/how-to-sketch-the-graph-and-find-continuity-of-functions.html
0 Response to "Sketch the Graph of a Function F That is Continuous on 1 5"
Post a Comment