The Precision Error in Reading, but the Error Increase

Error Analysis and Meaning Figures

Errors using inadequate information are much less than those using no data at all.

C. Babbage]

No measurement of a concrete quantity can be entirely authentic. It is important to know, therefore, only how much the measured value is likely to deviate from the unknown, true, value of the quantity. The art of estimating these deviations should probably be chosen uncertainty analysis, simply for historical reasons is referred to every bit error analysis. This document contains brief discussions well-nigh how errors are reported, the kinds of errors that can occur, how to estimate random errors, and how to conduct error estimates into calculated results. We are not, and volition not exist, concerned with the "percent mistake" exercises common in high school, where the student is content with computing the deviation from some allegedly authoritative number.

You might as well exist interested in our tutorial on using figures (Graphs).

Pregnant figures

Whenever y'all make a measurement, the number of meaningful digits that you lot write down implies the error in the measurement. For instance if you say that the length of an object is 0.428 m, you lot imply an incertitude of almost 0.001 thousand. To record this measurement as either 0.4 or 0.42819667 would imply that you only know it to 0.1 m in the first instance or to 0.00000001 m in the 2d. You should only report as many significant figures equally are consistent with the estimated fault. The quantity 0.428 m is said to take three pregnant figures, that is, three digits that make sense in terms of the measurement. Notice that this has nothing to do with the "number of decimal places". The aforementioned measurement in centimeters would exist 42.eight cm and still be a three significant figure number. The accepted convention is that simply one uncertain digit is to exist reported for a measurement. In the example if the estimated error is 0.02 m y'all would written report a result of 0.43 ± 0.02 thousand, not 0.428 ± 0.02 m.

Students often are dislocated almost when to count a nix as a meaning figure. The rule is: If the zero has a non-zero digit anywhere to its left, and then the nada is pregnant, otherwise it is non. For example 5.00 has three meaning figures; the number 0.0005 has merely ane significant figure, and ane.0005 has 5 significant figures. A number like 300 is not well divers. Rather i should write iii 10 tenⁱⁱ, one significant figure, or three.00 x 10², 3 significant figures.

Absolute and relative errors

The absolute error in a measured quantity is the dubiousness in the quantity and has the same units every bit the quantity itself. For example if you lot know a length is 0.428 chiliad ± 0.002 k, the 0.002 m is an absolute error. The relative mistake (as well chosen the partial fault) is obtained by dividing the absolute error in the quantity by the quantity itself. The relative error is usually more significant than the accented error. For case a i mm fault in the diameter of a skate cycle is probably more serious than a 1 mm fault in a truck tire. Note that relative errors are dimensionless. When reporting relative errors it is usual to multiply the fractional error by 100 and report information technology equally a percentage.

Systematic errors

Systematic errors arise from a flaw in the measurement scheme which is repeated each fourth dimension a measurement is made. If you do the same thing incorrect each time you make the measurement, your measurement volition differ systematically (that is, in the same direction each fourth dimension) from the correct result. Some sources of systematic error are:

Errors in the calibration of the measuring instruments.
Incorrect measuring technique: For case, one might make an incorrect scale reading because of parallax error.
Bias of the experimenter. The experimenter might consistently read an instrument incorrectly, or might permit knowledge of the expected value of a result influence the measurements.

It is clear that systematic errors do not average to zero if y'all average many measurements. If a systematic error is discovered, a correction can be made to the data for this mistake. If you measure a voltage with a meter that later turns out to have a 0.2 V kickoff, you tin can correct the originally determined voltages by this amount and eliminate the mistake. Although random errors tin exist handled more or less routinely, there is no prescribed way to find systematic errors. Ane must simply sit down and think almost all of the possible sources of mistake in a given measurement, and then do small experiments to run into if these sources are agile. The goal of a good experiment is to reduce the systematic errors to a value smaller than the random errors. For instance a meter stick should take been manufactured such that the millimeter markings are positioned much more than accurately than one millimeter.

Random errors

Random errors arise from the fluctuations that are virtually easily observed past making multiple trials of a given measurement. For example, if yous were to measure out the catamenia of a pendulum many times with a cease picket, y'all would observe that your measurements were not always the aforementioned. The main source of these fluctuations would probably be the difficulty of judging exactly when the pendulum came to a given point in its movement, and in starting and stopping the terminate watch at the time that you judge. Since you would not get the same value of the period each fourth dimension that you try to measure information technology, your effect is obviously uncertain. There are several common sources of such random uncertainties in the type of experiments that y'all are likely to perform:

Uncontrollable fluctuations in initial conditions in the measurements. Such fluctuations are the chief reason why, no matter how skilled the actor, no private tin toss a basketball game from the free throw line through the hoop each and every fourth dimension, guaranteed. Pocket-sized variations in launch weather or air motion crusade the trajectory to vary and the ball misses the hoop.
Limitations imposed by the precision of your measuring apparatus, and the uncertainty in interpolating between the smallest divisions. The precision simply means the smallest amount that can be measured straight. A typical meter stick is subdivided into millimeters and its precision is thus one millimeter.
Lack of precise definition of the quantity beingness measured. The length of a table in the laboratory is non well defined after information technology has suffered years of use. Y'all would find different lengths if yous measured at different points on the table. Another possibility is that the quantity beingness measured as well depends on an uncontrolled variable. (The temperature of the object for example).
Sometimes the quantity yous measure is well defined but is subject to inherent random fluctuations. Such fluctuations may be of a quantum nature or arise from the fact that the values of the quantity beingness measured are determined past the statistical beliefs of a large number of particles. Another example is Ac noise causing the needle of a voltmeter to fluctuate.

No matter what the source of the uncertainty, to be labeled "random" an uncertainty must have the belongings that the fluctuations from some "true" value are every bit likely to be positive or negative. This fact gives us a primal for understanding what to exercise about random errors. You lot could make a big number of measurements, and average the result. If the uncertainties are really equally likely to be positive or negative, you would look that the average of a big number of measurements would be very near to the correct value of the quantity measured, since positive and negative fluctuations would tend to cancel each other.

Estimating random errors

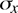At that place are several ways to make a reasonable guess of the random error in a detail measurement. The best manner is to brand a series of measurements of a given quantity (say, x) and summate the hateful, and the standard divergence from this data. The mean is defined as

where x _i is the issue of the i ^th measurement and N is the number of measurements. The standard departure is given by

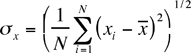
If a measurement (which is subject only to random fluctuations) is repeated many times, approximately 68% of the measured valves volition fall in the range.

We become more than sure that , is an authentic representation of the true value of the quantity x the more we repeat the measurement. A useful quantity is therefore the standard deviation of the mean defined equally . The quantity is a proficient judge of our uncertainty in . Notice that the measurement precision increases in proportion to as we increase the number of measurements. Non simply accept you lot made a more accurate determination of the value, you besides have a set of data that will allow you to estimate the dubiousness in your measurement.

The following example will clarify these ideas. Presume yous fabricated the following five measurements of a length:

	Length (mm)	Deviation from the mean
	22.8	0.0
	23.one	0.3
	22.seven	0.1
	22.vi	0.two
	23.0	0.2
sum	114.2	0.18	sum of the squared deviations
	split up past 5	divide by 5 and take the square root	(N = number information points = 5)
mean	22.8	0.xix	standard deviation
		divide past
		0.08	standard deviation of the mean

Thus the outcome is 22.84 ± .08 mm. (Notice the use of significant figures).

In some cases, it is scarcely worthwhile to echo a measurement several times. In such situations, you often tin can judge the error by taking account of the to the lowest degree count or smallest division of the measuring device. For example, when using a meter stick, i can measure to perhaps a half or sometimes even a fifth of a millimeter. And so the absolute error would be estimated to be 0.five mm or 0.2 mm.

In principle, you lot should by one means or another estimate the dubiety in each measurement that you make. But don't make a big production out of information technology. The essential idea is this: Is the measurement good to about 10% or to about 5% or 1%, or even 0.one%? When you accept estimated the error, you will know how many significant figures to employ in reporting your upshot.

Propagation of errors

In one case yous take some experimental measurements, you usually combine them according to some formula to make it at a desired quantity. To find the estimated error (dubiety) for a calculated effect one must know how to combine the errors in the input quantities. The simplest procedure would be to add together the errors. This would be a bourgeois assumption, but information technology overestimates the doubtfulness in the result. Clearly, if the errors in the inputs are random, they volition abolish each other at least some of the time. If the errors in the measured quantities are random and if they are contained (that is, if one quantity is measured as being, say, larger than it really is, another quantity is still just equally probable to be smaller or larger) then fault theory shows that the uncertainty in a calculated consequence (the propagated error) tin can be obtained from a few elementary rules, some of which are listed in Table 1. For example if two or more numbers are to be added (Tabular array i, #2) then the absolute error in the event is the square root of the sum of the squares of the absolute errors of the inputs, i.east.

and so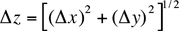

In this and the post-obit expressions, and are the absolute random errors in x and y and is the propagated uncertainty in z. The formulas do not apply to systematic errors.

The full general formula, for your data, is the following;

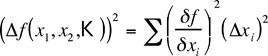
It is discussed in item in many texts on the theory of errors and the analysis of experimental data. For now, the collection of formulae in tabular array 1 will suffice.

Tabular array 1: Propagated errors in z due to errors in x and y. The errors in a, b and c are assumed to exist negligible in the following formulae.

Case	Function	Propagated fault
ane)	z = ax ± b
ii)	z = x ± y
3)	z = cxy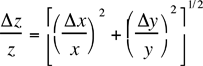
4)	z = c(y/x)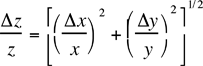
5)	z = cx^a
vi)	z = cx^ay^b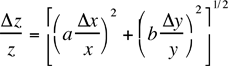
vii)	z = sinten
8)	z = cosx
nine)	z = tan10